Effektivwert
Einleitung
Kurz erklärt ist der Effektivwert der Wirksame – der eben effektive Wert des Wechselstromes.
Formelzeichen

Einheit

Formeldreieck

–

Einführung
Der Effektivwert gibt den Wert an den der Gleichstrom haben müsste damit der Wechselstrom & der Gleichstrom die gleiche Wärmewirkung haben.

D.h. Schickt man einen Gleichstrom durch einen Verbraucher entsteht eine bestimmte Menge an Wärme.
Schicken wir nun Wechselstrom durch den Verbraucher, ist der Effektivwert der Wert des Wechselstroms, der Wert bei dem die gleiche Menge an Wärme entsteht wie bei dem Gleichstrom.
Praktisch
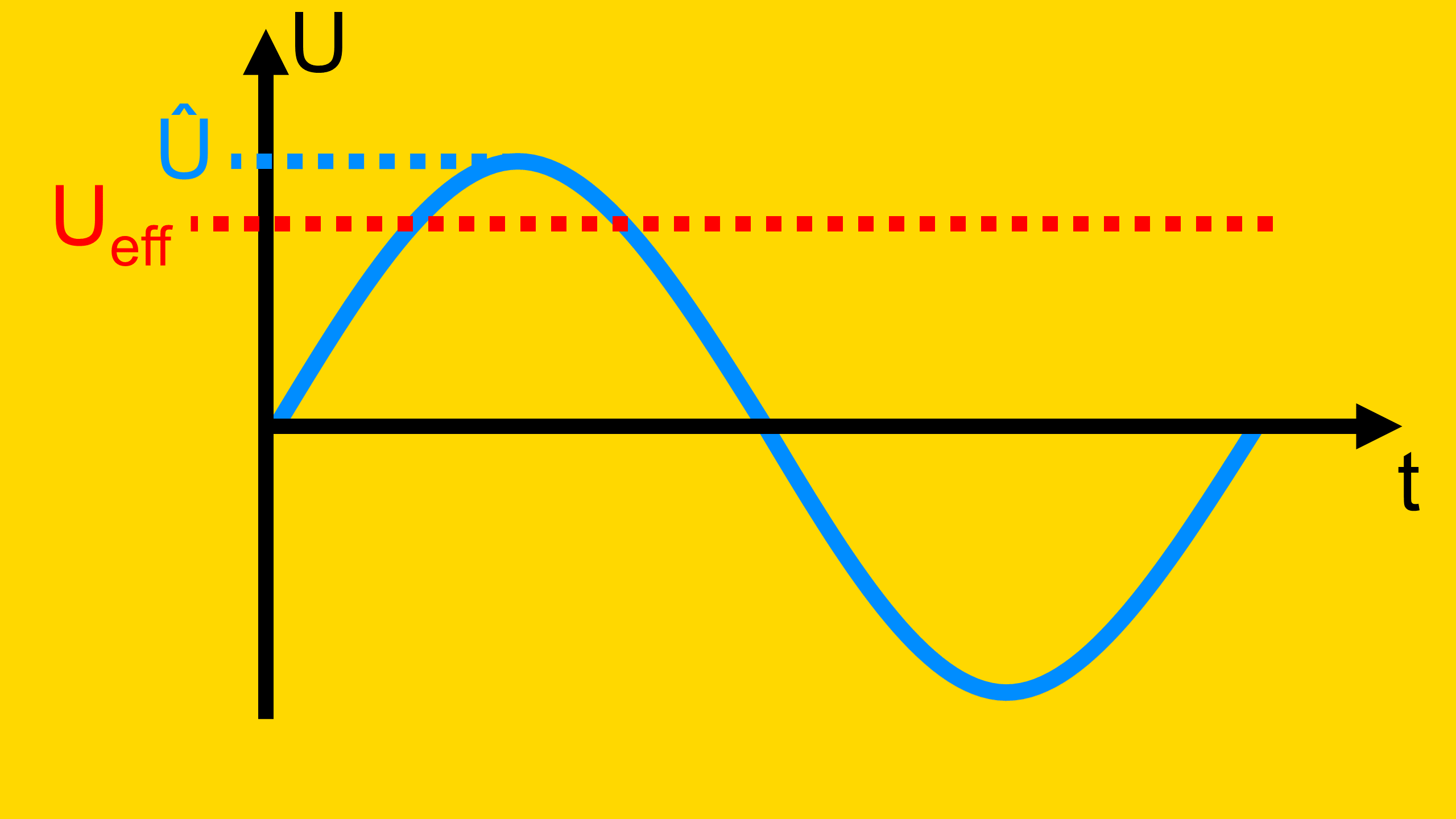
Bei einer sinusförmigen Wechselspannung liegt der Effektivwert etwas unter dem Spitze-Wert. Im unten stehenden Bild ist dies gezeigt. Um den genauen Effektivwert zu erhalten, muss man diesen errechnen. Dies wird im Folgenden näher erklärt.
Berechnung
Um den Effektivwert zu berechnen gibt es eine Formel die da lautet:
Ueff = U spitze / crest faktor
Crest Faktor kurzgesagt: Je nachdem welche Form der Spannungsverlauf hat, ist der Crest Faktor anders.
Beispielsweise hat die Sinusförmige Wechselspannung den crestfaktor von √2
⇨ Crest Faktor
Somit würde die Formel hier heißen Ueff = U spitze / √2
Ein Weiteres Beispiel: Eine Dreicksspannung hat den crest wert von √3.
Hier würde die Formel lauten Ueff = Uspitze / √3.
Formeldreieck
Um sich die Formel besser merken zu können gibt es hierfür auch ein Formeldreick. Dabei ist Û (U-Spitze) in der Spitze, Unten ist Ueffektiv und der crest faktor z.B. √2.
Beispiel
geg.: Wie im Bild gezeigt ist eine sinusförmige Wechselspannung mit dem Spitzenwert von 5V gegeben.
ges.: Der Effektivwert dieser Spannung.
Berechnung:
Ueff = 5V / √2 =
Ergebnis:
Ueff =