Stabilität
Einleitung
Damit eine Regelung funktioniert, muss diese stabil sein.
Um die Stabilität eines Regelkreises zu bestimmen, werden die Polstellen bestimmt. Mithilfe der Polstellen kann dann eine Aussage über die Stabilität des Systems getroffen werden.
⇨ Polstellen einfach erklärt
Überblick – Was ist Stabilität?
Ein Regelkreis kann in Bezug auf die Stabilität in 3 Kategorien eingeordnet werden.
Diese, sowie das Prinzip, ist im untenstehenden Bild genauer beschrieben.
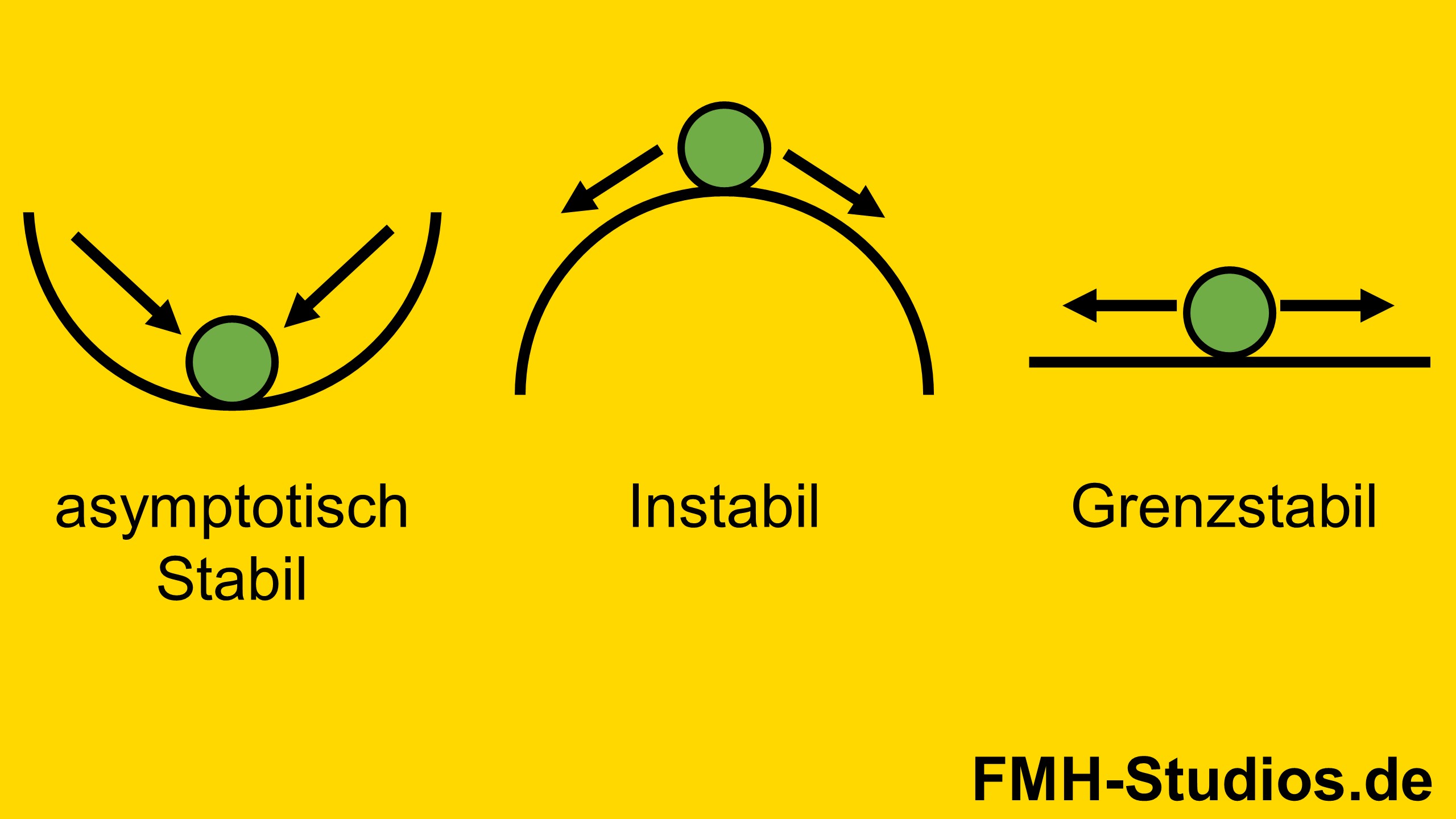
1. Fall: Stabil: Bei Anregung des Balls, wird dieser am Anfang evtl. in der Schale hin und her rollen, am Ende wird er aber still am Boden der Schale liegen bleiben.
2. Fall: Grenzstabil: Bei Anregung des Balls, wird dieser nie in den Anfangszustand zurückkehren aber er kann einen festen Zustand annehmen.
3. Fall: Instabil: Bei Anregung des Balls, wird dieser nie in den Anfangszustand zurückkehren und er wird keinen festen Zustand annehmen
In Bezug auf die Zeit lässt sich die Stabilität ebenfalls darstellen:
[Bild folgt]
Pol-Nullstellen-Diagramm – Stabilität
Um nun die Stabilität eines Regelkreises zu bestimmen, werden wie bereits erwähnt, die Polstellen analysiert.
Konkret wird ein Pol-Nullstellen-Diagramm angefertigt.
Wie das geht ist hier näher beschrieben:
⇨ Pol-Nullstellen-Diagramm
Das Pol-Nullstellen-Diagramm kann in 2 Bereiche unterteilt werden.
Die linken S-Halbebene und die rechte S-Halbebene.
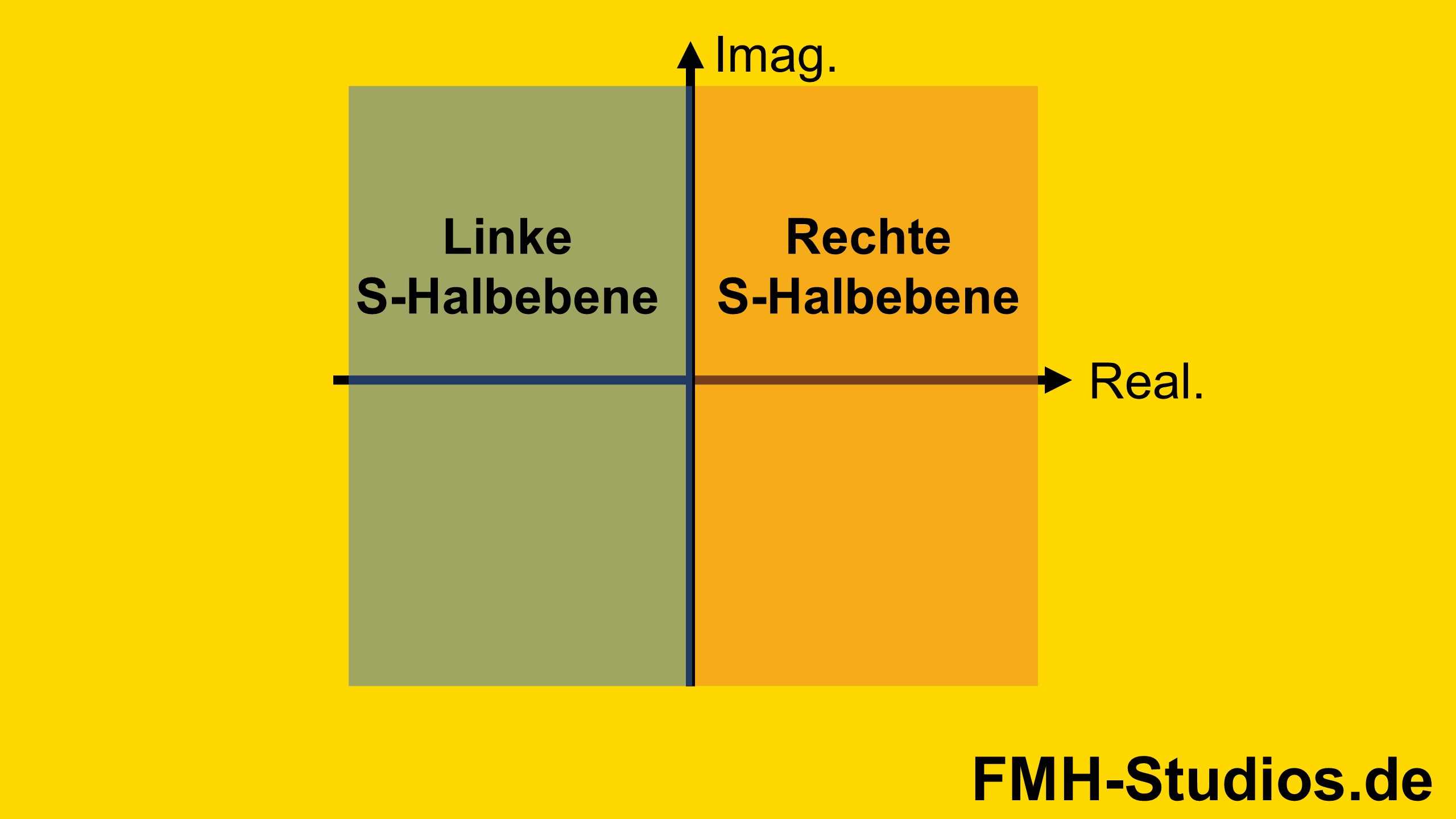
Abhängig davon wo die Polstellen liegen, verhält sich das System anders. Im Folgenden ist der Zusammenhang aus Pol-Nullstellen Diagramm und dem Zeitlichen Verlauf gezeigt.
[Bild folgt]
Je nachdem wo die Polstellen liegen, wird das System als Stabil, grenzstabil oder instabil bezeichnet.
Dies wird im Folgenden näher beschrieben.
Stabil
Ein System welches asymptotisch Stabil ist, kehrt nach Anregung von selbst wieder in den Anfangszustand zurück.
Ein System gilt dann als stabil, wenn alle Polstellen auf der linken S-Halbebene liegen.
[Bild folgt]
Grenzstabil
Wenn das System Grenzstabil ist, kehrt nach Anregung nicht von selbst wieder in den Anfangszustand zurück, bleibt aber begrenzt.
Bei einem Grenzstabilen System muss mindestens eine Polstelle auf der Imaginär-Achse liegt. Es darf aber keine Polstelle in der rechten s-Halbebene liegt.
[Bild folgt]
Instabil
Ist das System Instabil ist, kehrt es nach Anregung von selbst nicht wieder in den Anfangszustand zurück und bleibt nicht begrenzt.
Instabil ist ein System sobald mindestens eine Polstelle auf der rechten s-Halbebene liegt.
[Bild folgt]