Herleitung der Übertragungsfunktion des klassischen Regelkreises
In der untenstehenden Abbildung ist ein klassischer Regekreis dargestellt. Die Rückführung ist als Gegenkopplung realisiert.
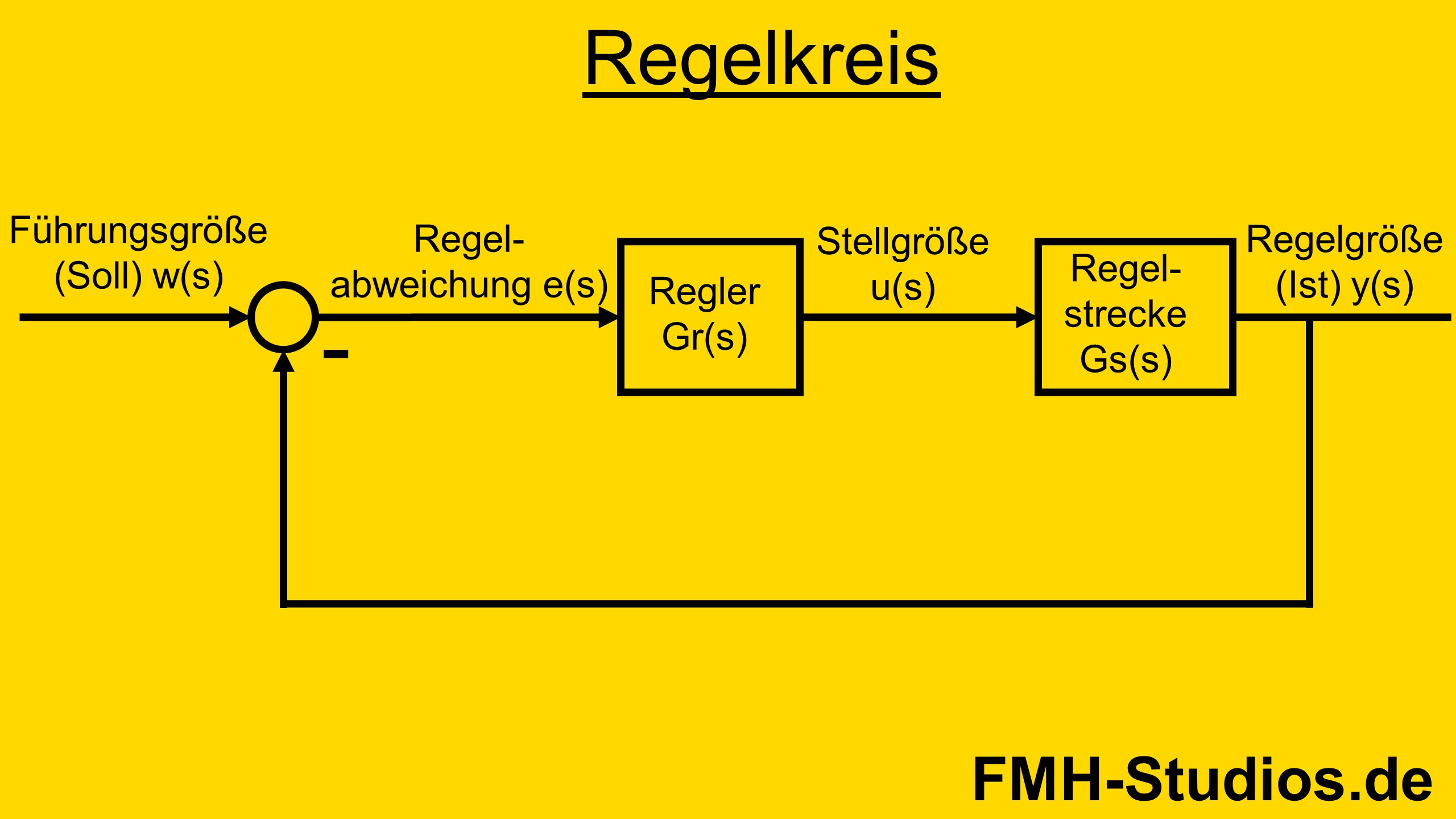
Das System besteht aus Regler Gr(s) und Strecke Gs(s).
Eine Übertragungsfunktion ergibt sich durch folgende Gleichung:
G(s) = Ausgang y(s) / Eingang w(s).

Denn Eingang * Übertragungsfunktion gibt Ausgang.
Genauere Erklärung was die Übertragungsfunktion ist:
⇨ Was ist eine Übertragungsfunktion
Nun soll die Übertragungsfunktion mit den Regelkreis-Gliedern ausgedrückt werden.
Hierfür wird zunächst betrachtet wie sich der Ausgang ergibt. Regelabweichung e(s) * Regler Gr(s) * Strecke Gs(s). Dies wird entsprechend in den Zähler geschrieben.
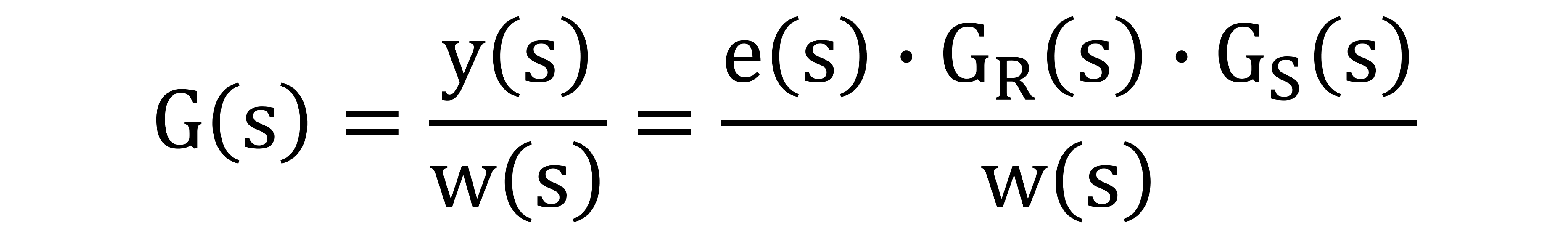
Für den Eingang wird sich die Differenzbildung angeschaut.
w(s) – y(s) = e(s) | + y(s)
w(s) = e(s) + y(s)
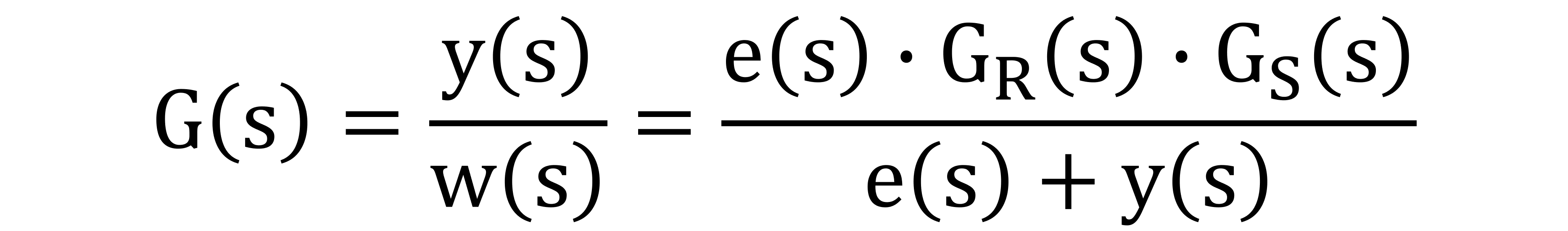
Anschließend wird für den Ausgang y(s) die oben ermittelte Gleichung eingesetzt.
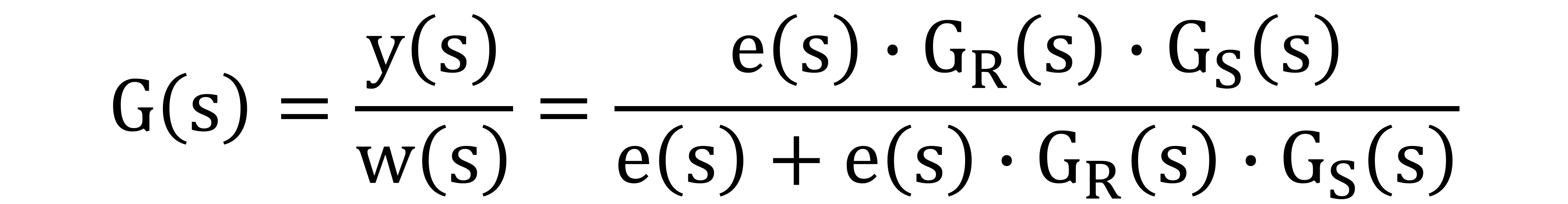
Wie man sieht kürzt sich nun die Regelabweichung e(s) heraus.
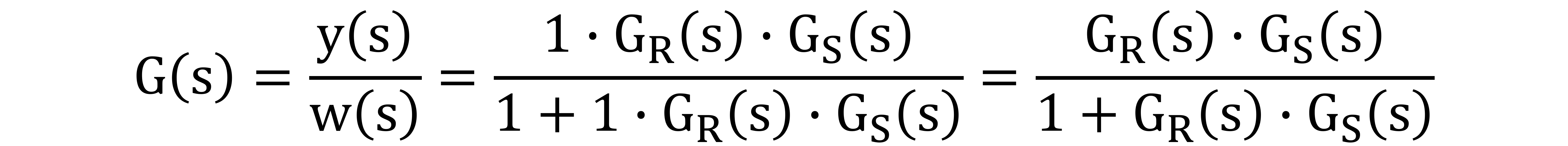
Vergleicht man das Ergebnis mit dem Ergebnis welches über die einfache Herangehensweise ermittelt wurden, gleichen sich beide Ergebnisse.
⇨ Übertragungsfunktion Regelkreis
Hinweis:
Kommt nun die Frage auf wie man bei einem beliebigen System auf diese Herleitung bzw. auf die Anfangsgleichung kommt, ist die Antwort:
Grundsätzlich ist egal wie man die Gleichungen setzt. Man hätte auch die Ausgangsgleichung mit der Stellgröße u(s) * Regelstrecke Gs(s) bilden können. Anschließend die Eingangsgleichung auf mit der Stellgröße u(s). Schlussendlich wäre das gleiche Ergebnis herausgekommen.
Herleitung der Übertragungsfunktion eines Regelkreises mit Mitkopplung
In der unten dargestellten Abbildung ist ein Regelkreis mit einer Mitkopplung zu sehen. Hierbei ist bei dem Vergleicher keine Subtraktion sondern eine Multiplikation. (Dies sorgt im Regelsystem für ein Instabiles Verhalten, dies stellt in diesem Beitrag aber keine Relevanz dar.)
⇨ Mitkopplung im Regelkreis
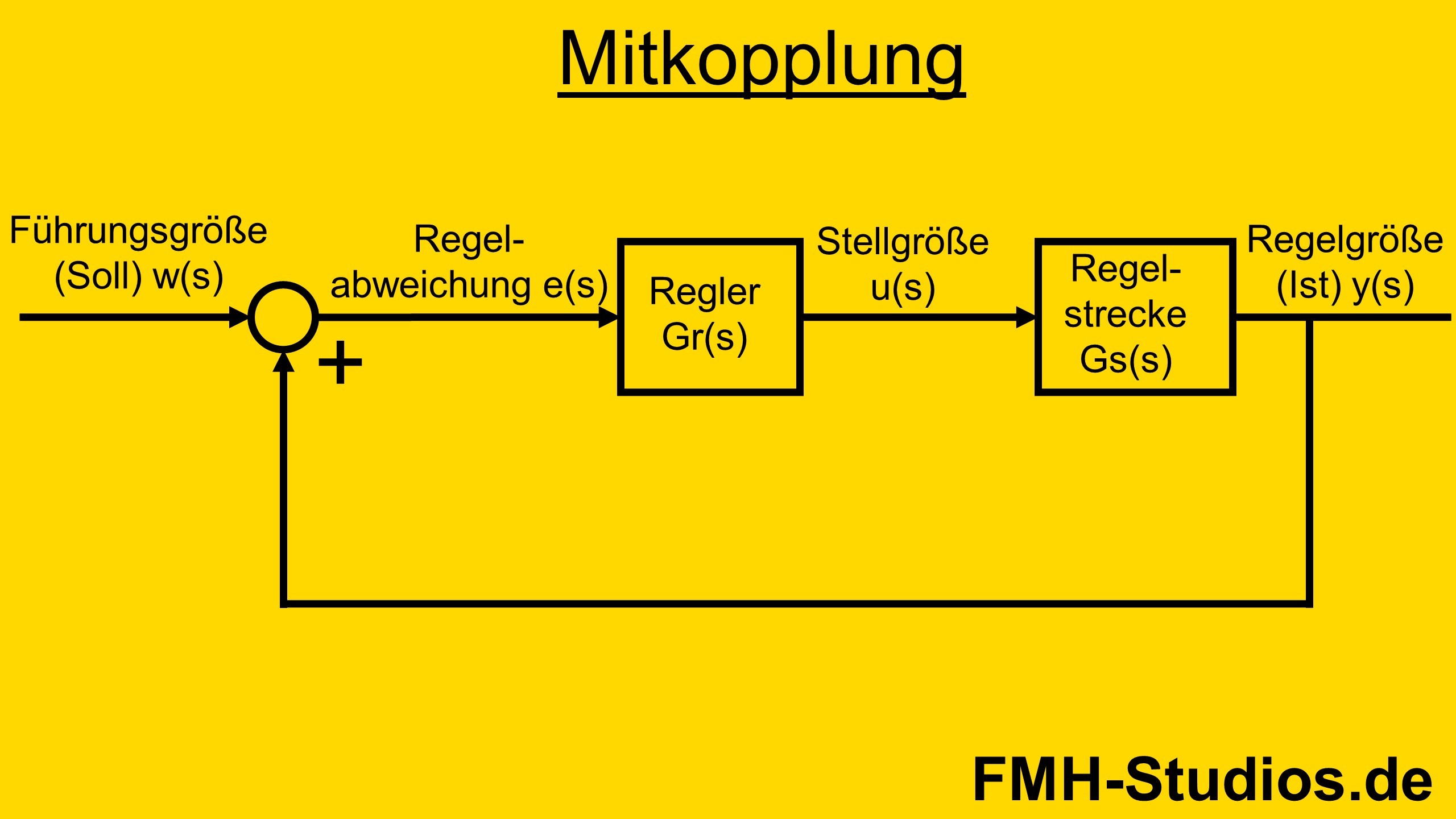
Das Vorgehen zur Erstellung der Übertragungsfunktion ist dasselbe.
Auch hier ergibt sich die Übertragungsfunktion durch folgende Gleichung:
G(s) = Ausgang y(s) / Eingang w(s)

.
Denn Eingang * Übertragungsfunktion gibt Ausgang.
Genauere Erklärung was die Übertragungsfunktion ist:
⇨ Was ist eine Übertragungsfunktion
Nun soll die Übertragungsfunktion mit den Regelkreis-Gliedern ausgedrückt werden.
Hierfür wird wieder mit dem Ausgang begonnen. Dieser kann wie folgt beschrieben werden. Regelabweichung e(s) * Regler Gr(s) * Strecke Gs(s). Dies wird entsprechend in den Zähler geschrieben.
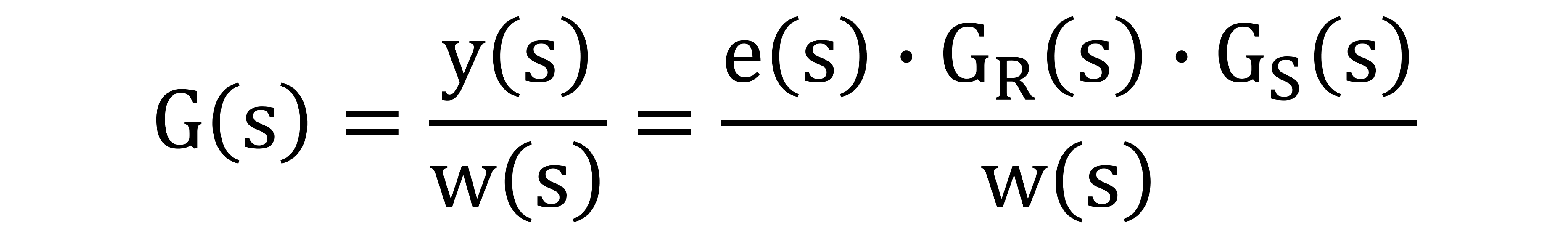
Für den Eingang wird hier zunächst auch der Vergleicher angeschaut.
w(s)+y(s) = e(s) |-y(s)
w(s) = e(s) – y(s)
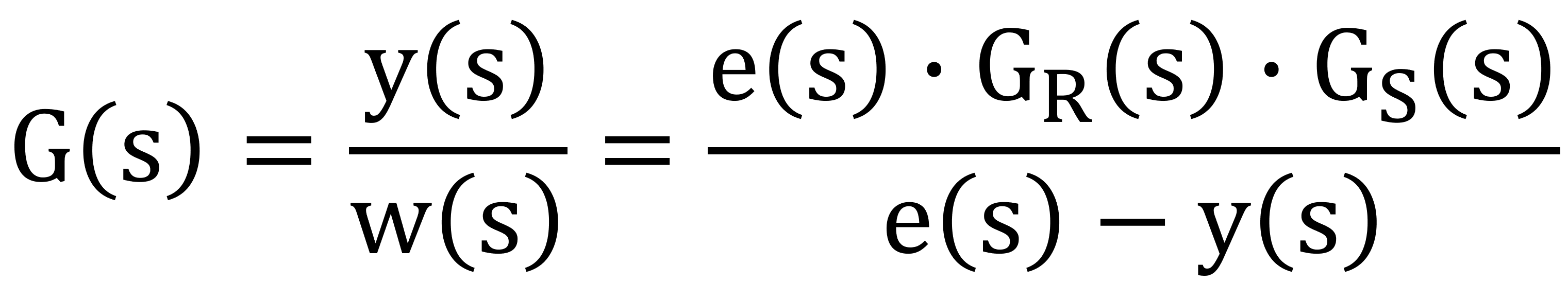
Anschließend wird für den Ausgang y(s) die oben ermittelte Gleichung eingesetzt.

Wie man sieht kürzt sich nun die Regelabweichung e(s) heraus.
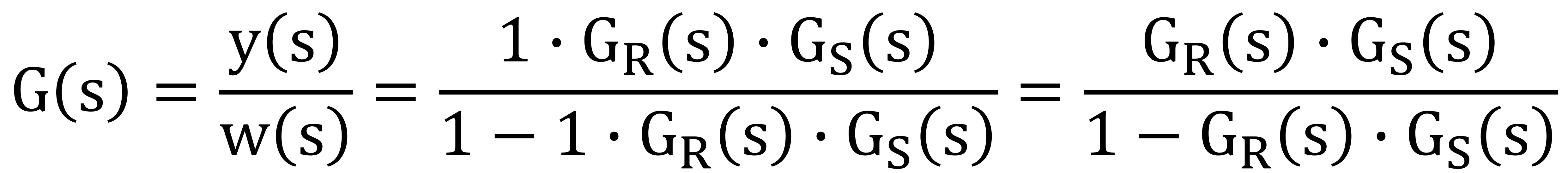
Im vergleich zum Klassischen Regelkreis ändert sich einfach das Rechenzeichen im Nenner.