Spezifische Leitfähigkeit
Einleitung
Die spezifische Leitfähigkeit eines Halbleiters ist abhängig von der Beweglichkeit der Ladungsträger und von der Ladungsträgerdichte. Beide Parameter sind auch stark temperaturabhängig, wodurch die Leitfähigkeit ebenfalls temperaturabhängig ist.
Im Folgenden Artikel soll der Zusammenhang zwischen den bereits angesprochenen Themen näher erklärt werden und auch ein allgemeines Verständnis zur Leitfähigkeit des Halbleiters erlangt werden.
Erklärung – Leitfähigkeit im Halbleiter
Die Leitfähigkeit im Halbleiter ist von 2 Parametern abhängig:
– Der Beweglichkeit der Ladungsträger
– Der Ladungsträgerdichte
(siehe unterer Abschnitt „Berechnung der spezifischen Leitfähigkeit)
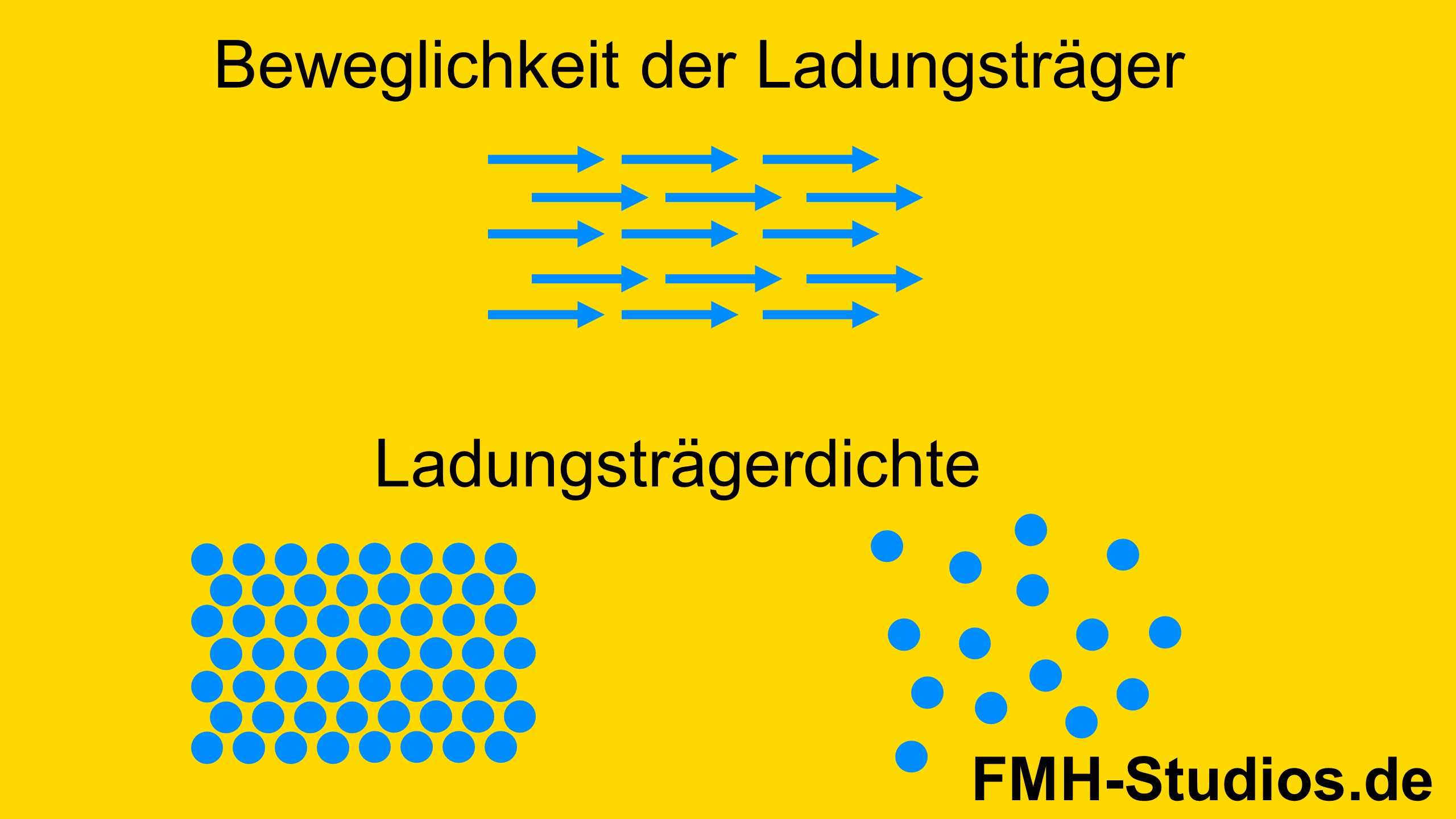
Die Beweglichkeit der Ladungsträger ist abhängig von:
– Temperatur und
– Dotierung
Die Ladungsträgerdichte eines Halbleiters ist abhängig von der Temperatur. Im Folgenden wird dies näher erläutert
Unterscheidung – Dotierter & Reiner Halbleiter
Bei dem Verhalten der Leitfähigkeit muss zunächst zwischen dotiertem und nicht dotiertem Halbleiter unterschieden werden.
Kurzgesagt: Beim reinen Halbleiter
Reiner (intrinsischer) Halbleiter
Bei einem nicht dotiertem – reinen Halbleiter ist bereits bekannt, dass bei niedrigen Temperaturen das Gitter fest ist, es somit keine freien Elektronen gibt und daher der Halbleiter nichtleitend ist. Durch Erhitzung lösen sich Elektronen aus der Gitterstruktur und dienen zum Ladungstransport.
⇨ Reiner (intrinsischer) Halbleiter
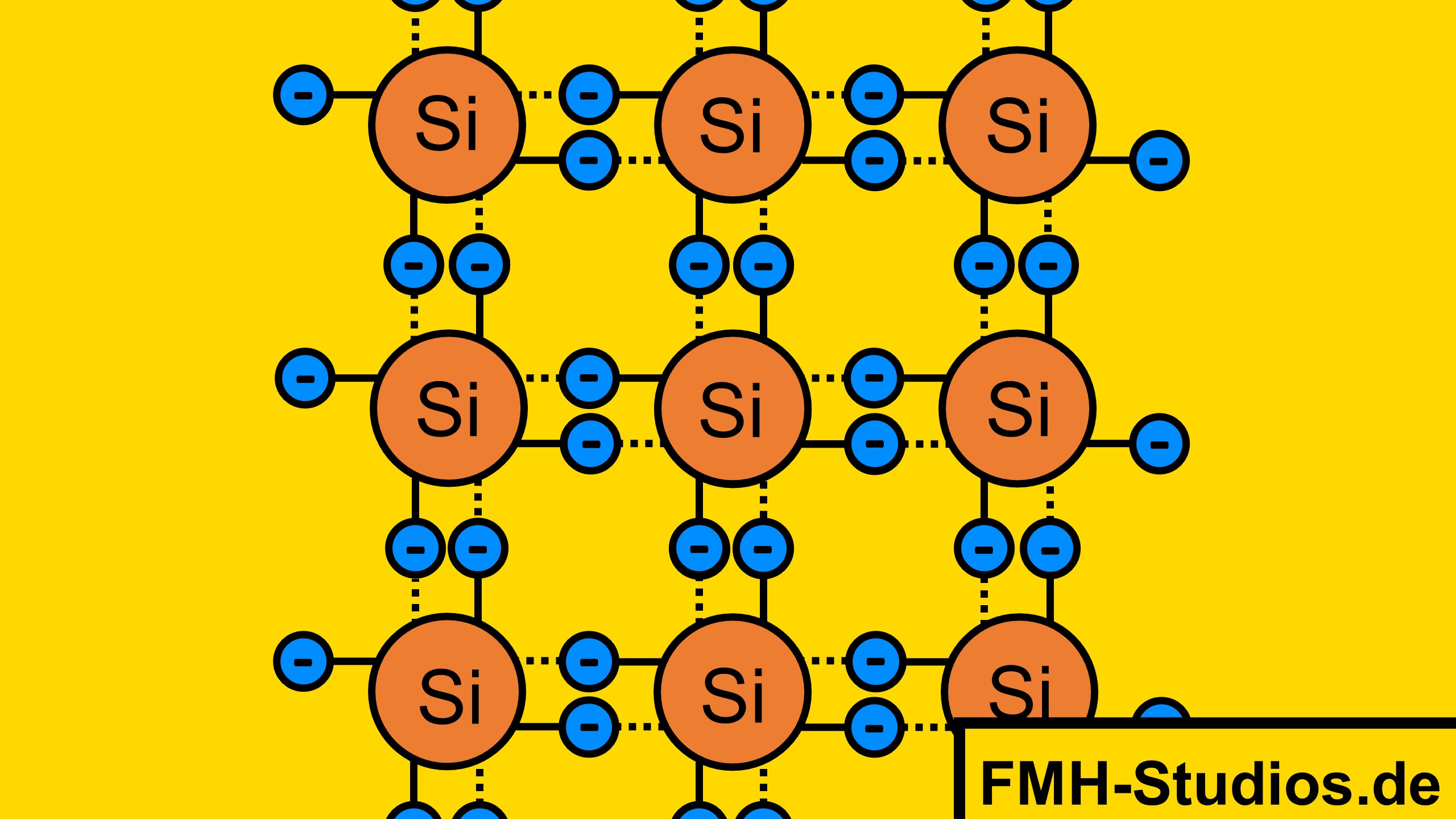
Man spricht hier von Eigenleitung. Im unteren Abschnitt wird genauer auf die Abhängigkeit zur Temperatur eingegangen.
Kennlinie / Funktion – Reiner Halbleiter (intrinsischer Halbleiter)
Das oben beschriebene Verhalten ist auch in der Kennlinie erkennbar. Bei niedrigen Temperaturen ist der Halbleiter nicht leitend. Ab einer bestimmten Temperatur jedoch steigt die spezifische Leitfähigkeit an und der Halbleiter wird leitend bzw. die spezifische Leitfähigkeit steigt an.

Dotierter Halbleiter
Beim dotierten Halbleiter wurden Fremdatome in den reinen Halbleiter eingebracht. Man spricht hier von sogenannten Störstellen.
⇨ Dotierung
Wie bereits erklärt gibt es beim n-dotierten Halbleiter durch das Fremdatom bereits bei niedrigen Temperaturen freie Elektronen.
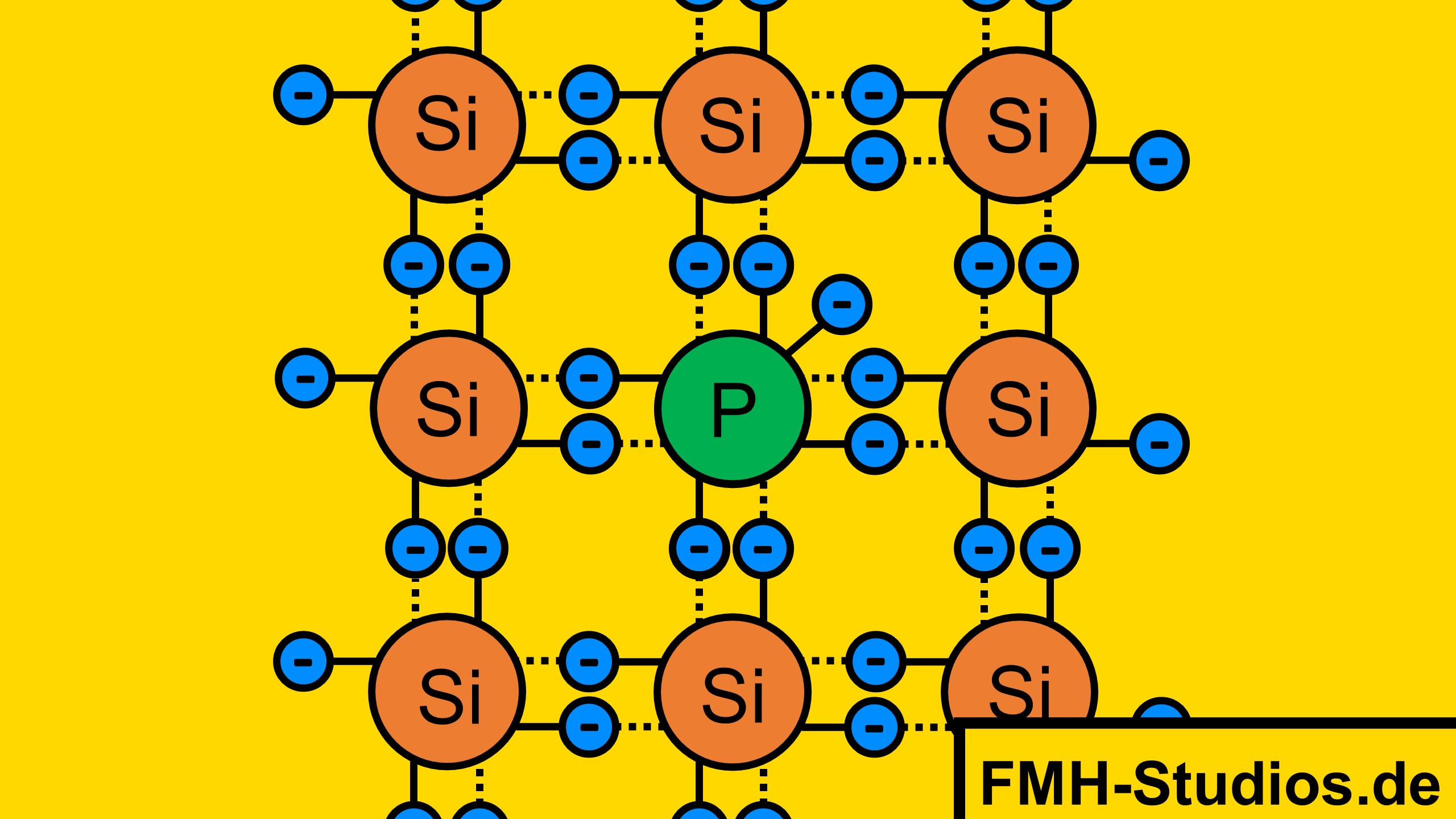
Allerdings können sich durch weitere Temperaturerhöhung (wie beim reinen Halbleiter auch) Elektronen aus dem Gitter lösen und zu freien Elektronen werden, die zum Ladungstransport beitragen.
Kennlinie / Funktion – Dotierter Halbleiter
Die spezifische Leitfähigkeit in Abhängigkeit zur Temperatur kann beim dotierten Halbleiter in 3 bzw. 4 Bereiche unterteilt werden.
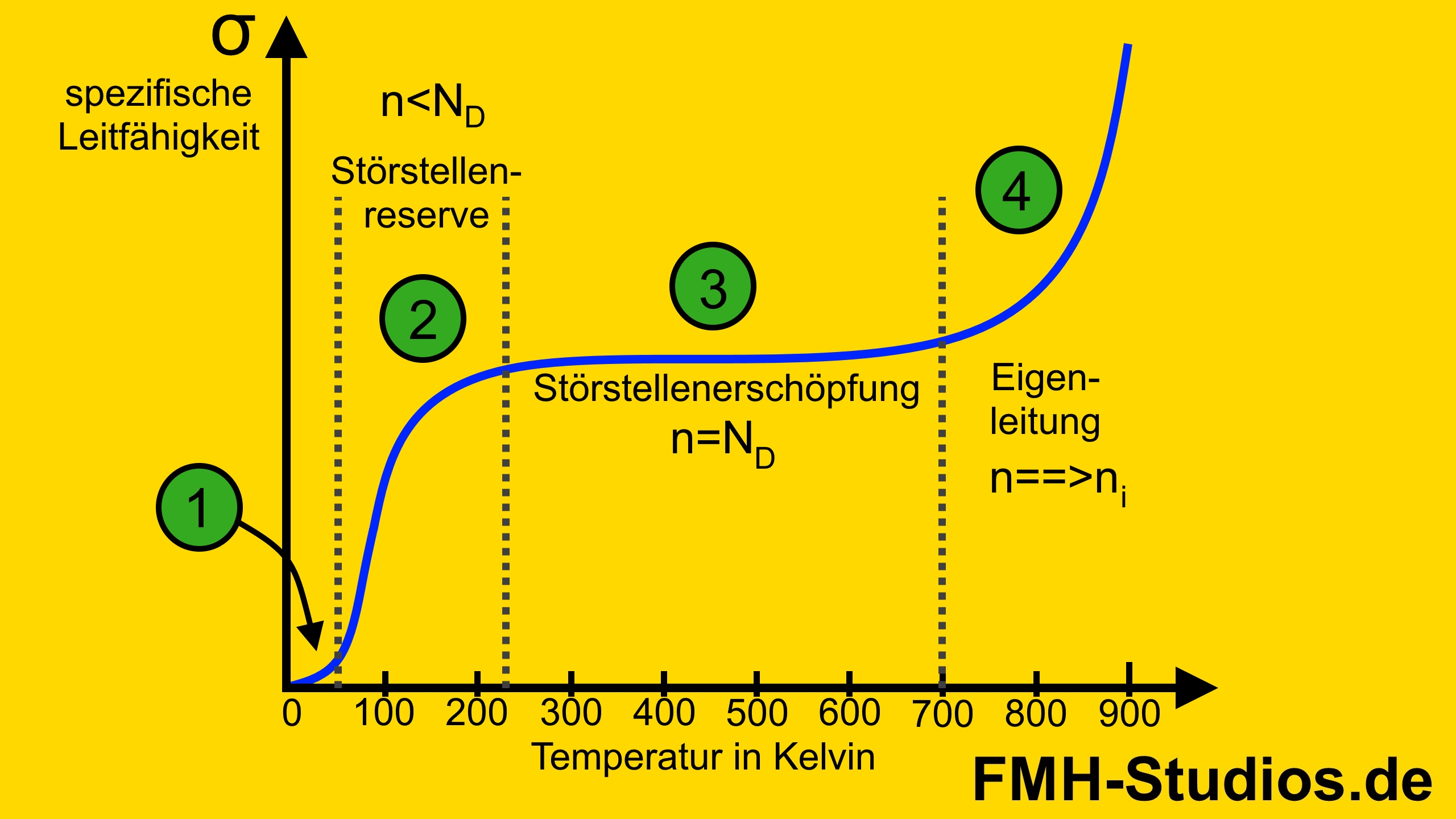
1. Temperatur zu niedrig
Bei sehr niedrigen Temperaturen (0K) gibt es keine freien Ladungsträger. Alle Elektronen sind noch fest gebunden und können sich nicht frei bewegen.
Entweder sind die Elektronen fest im Gitter gebunden (so wie auch beim nicht dotierten Halbleiter).
Die „überschüssigen“ Elektronen (welche nicht im Gitter gebunden sind) sind noch fest an die Dotieratome gebunden.
2. Störstellenreserve
Wird die Temperatur erhöht, lösen sich die „überschüssigen“ Elektronen (die nicht im Gitter gebunden sind) von den Dotieratomen und werden zu freien Elektronen.
Zunächst gilt: Je höher die Temperatur steigt, desto mehr Elektronen lösen sich von den Dotieratomen ab.
Fachlich: Die Donatoren werden ionisiert.
3. Störstellenerschöpfung
Irgendwann sind alle „überschüssigen“ Elektronen (die nicht im Gitter gebunden sind) frei. Auch wenn die Temperatur erhöht wird, können keine weiteren gelöst werden. Die spezifische Leitfähigkeit bleibt somit gleich, obwohl die Temperatur erhöht wird. Der Bereich der Störstellenerschöpfung liegt im Bereich zwischen -50°C < T < 200°C.
4. Eigenleitung
Ab einer bestimmten Temperatur lösen sich auch Elektronen aus dem Gitter. (So wie bei einem reinen Halbleiter). Man spricht dabei von Eigenleitung.
Die vorangegangene Erklärung bezog sich auf einen n-dotierten Halbleiter. Gleiches lässt sich, statt den Elektronen mit den Löchern, auf den p-dotierten Halbleiter übertragen.
Berechnung der spezifischen Leitfähigkeit
n-dotierte Halbleiter: σ_n=q ∙ µ_n∙ n
μn,p: Beweglichkeit der Elektronen bzw. Löcher
Die Beweglichkeit der Löcher liegt typischerweise
um den Faktor 2-3 unter der der Elektronen.
Elementarladung q= 1.6E-19 As