Diffusionsspannung
Einleitung
Werden N dotierter Halbleiter und P dotierter Halbleiter zusammengefügt, entsteht ein sogenannter PN-Übergang. Die freien Elektronen des N-Halbleiters und die freien Löcher des P-Halbleiters ziehen sich an. Sie verschmelzen zusammen. Diesen Vorgang nennt man Diffusion und das Verschmelzen nennt man Rekombination. Hierdurch bleiben nur noch die ortsfesten ionisierten Dotieratome zurück.
Diese weisen eine bestimmte Ladung auf.
Die Potentialdifferenz wird als Diffusionsspannung bezeichnet. Durch diese ergibt sich im Halbleiter ein Gleichgewicht.
Zusammenfassung – Erklärung Diffusionsspannung
Schritt 1: Freie Elektronen & freie Löcher ziehen sich an. Diffusion im Grenzgebiet. Es entsteht der sogenannte Diffusionsstrom. -> Diffusionsstrom.
Schritt 2: Freie Elektronen & freie Löcher verschmelzen. Rekombination.
Schritt 3: Ortsfeste Dotieratome bleiben zurück und sind nicht mehr im Gleichgewicht. Es entsteht eine Spannung. Die Diffusionsspannung.
Schritt 4: Je mehr Ladungsträger rekombinieren, desto größer wird die Diffusionsspannung.
Schritt 5: Durch die Diffusionsspannung entsteht ebenfalls ein Strom im PN-Übergang. Der sogenannte Driftstrom. Dieser fließt in die entgegengesetzte Richtung wie der Diffusionsstrom.
Schritt 6: Diffusionsstrom & Driftstrom fließen in entgegengesetzte Richtungen. Es stellt sich irgendwann ein Gleichgewicht ein.
Halbleiter Aufbau
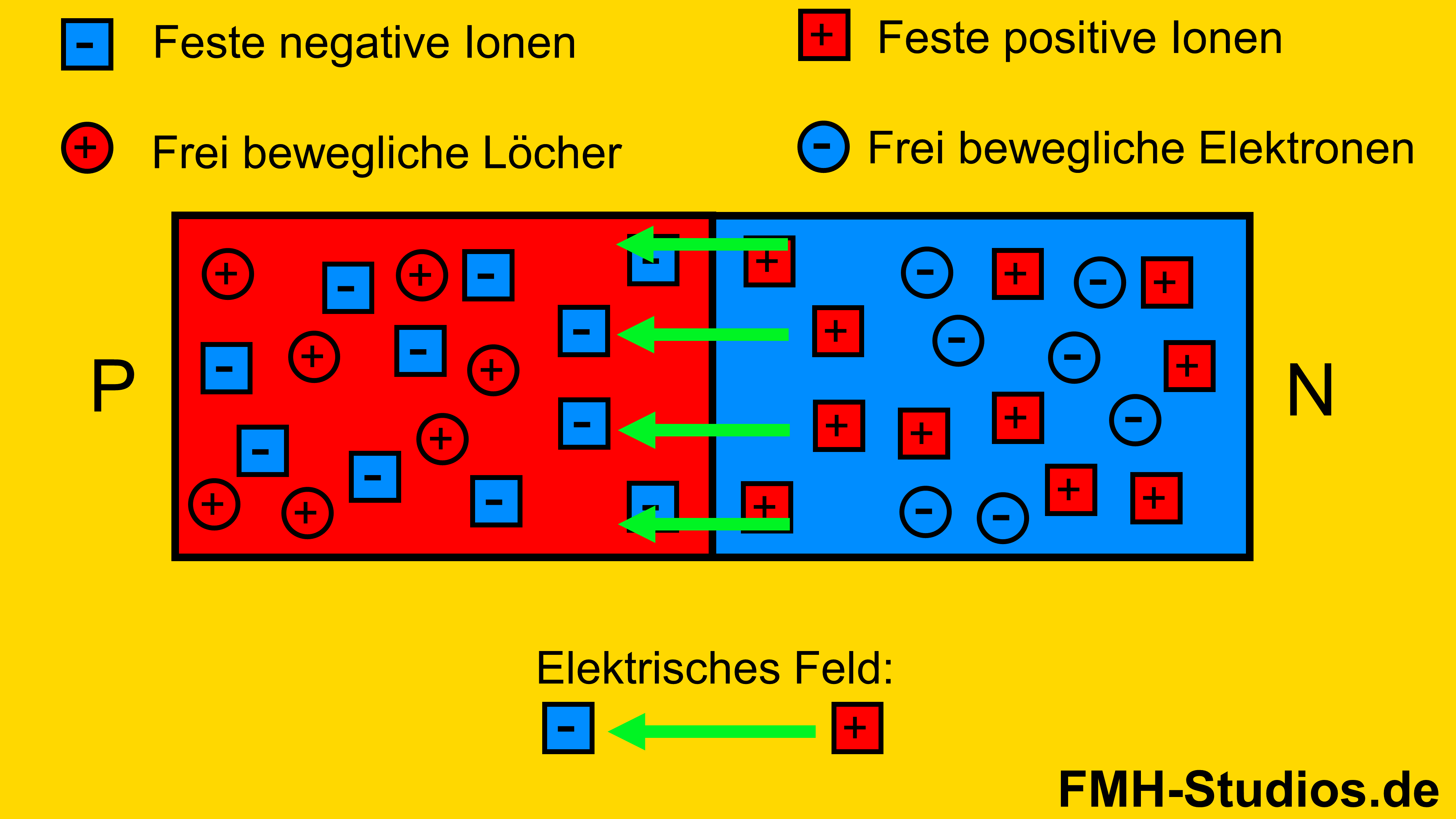
Im P-dotierten Halbleiter befinden sich freie Löcher und die ortsfesten Dotieratome, welche negativ geladen sind. In dem N-dotierten Halbleiter befinden sich freie Elektronen und die ortsfesten Dotieratome, welche positiv geladen sind.

Diffusionsstrom
Nach dem Zusammenfügen der beiden dotierten Halbleiter ziehen sich die freien Löcher und die freien Elektronen an.
Die negative Ladung des Elektrons und die positive Ladung des Lochs ziehen sich an.
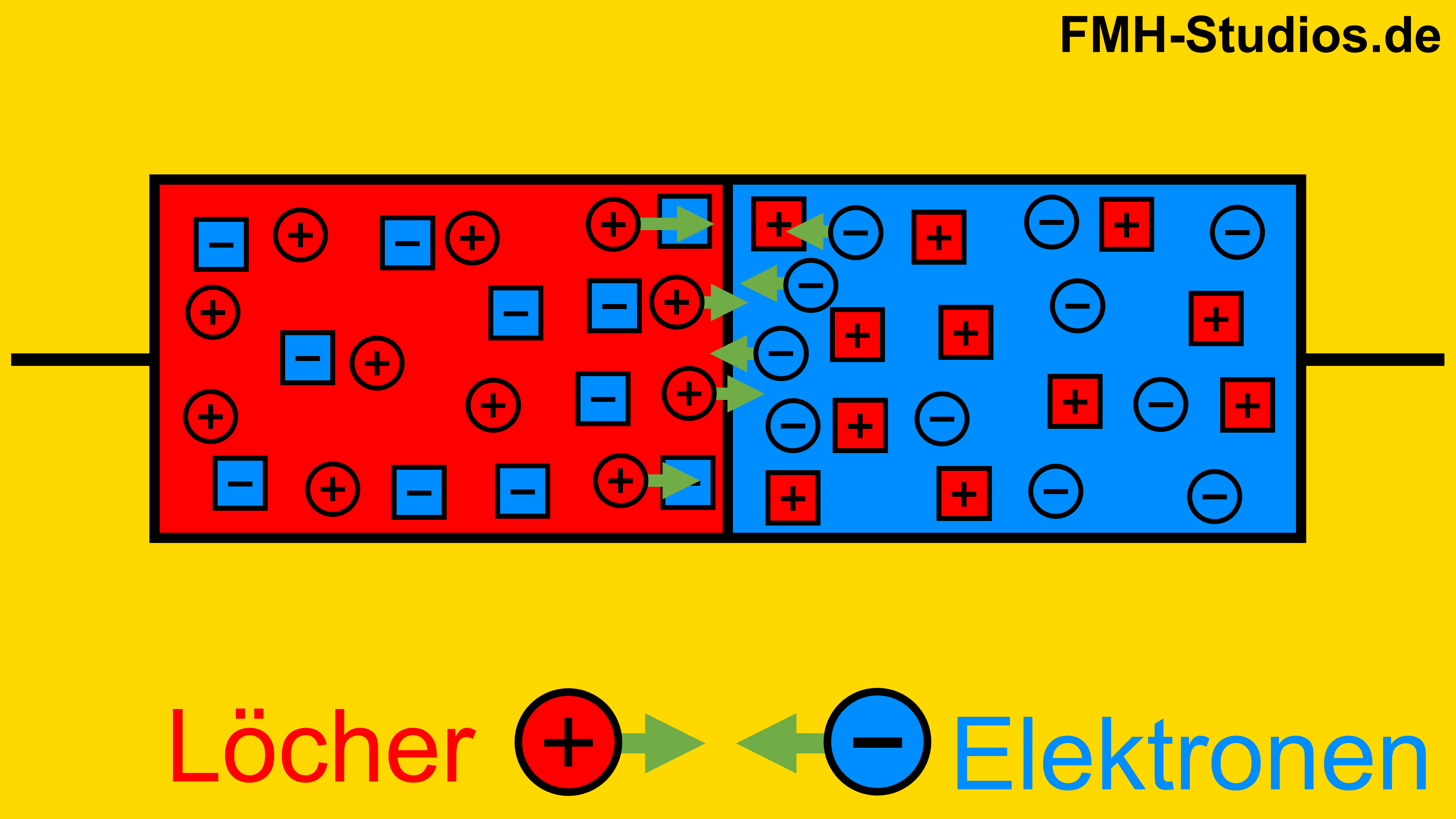
Das freie Elektron setzt sich anschließend in das freie Loch. Dieser Vorgang wird als Rekombination bezeichnet.
Beide Ladungsträger, also freies Elektron und freies Loch, sind dann sozusagen neutralisiert und können in der Darstellung entfernt werden.
So bildet sich die sogenannte Raumladungszone.
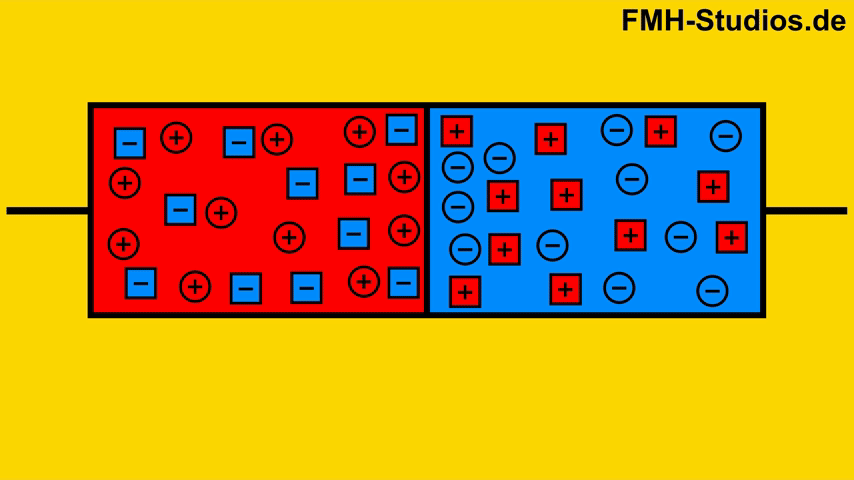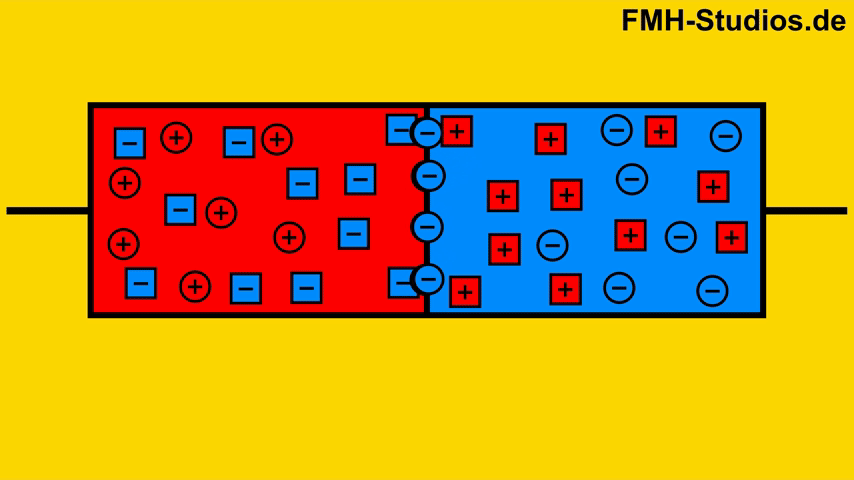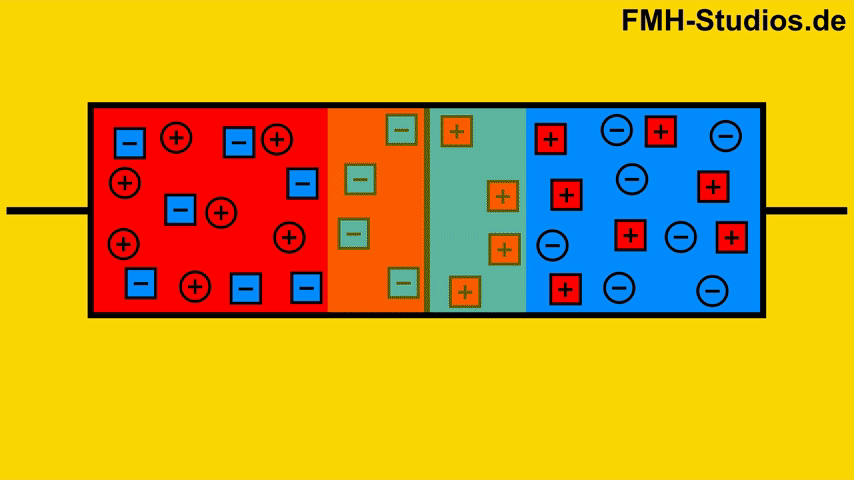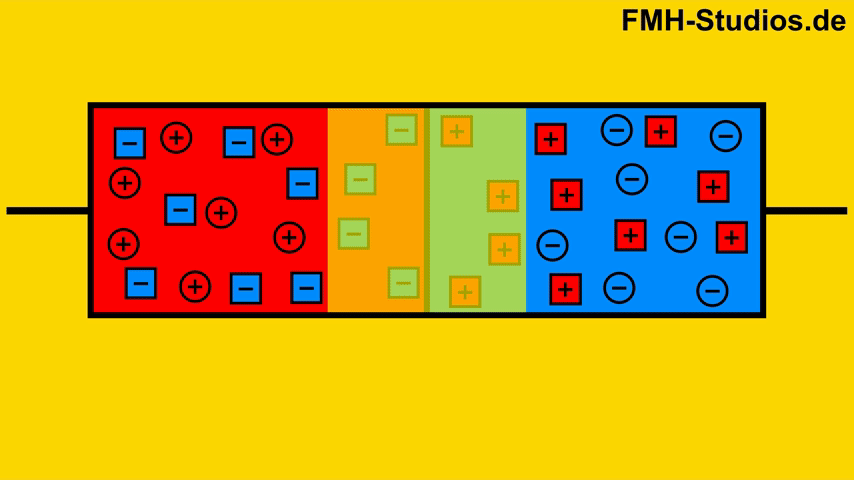
Entstehung der Diffusionsspannung
Durch den Diffusionsstrom und die dadurch resultierende Rekombination an der Grenze verschwinden aus beiden Bereichen die freien Elektronen und Löcher. Übrig bleiben nur noch die entsprechenden Ionen. Durch die übrigbleibenden Ionen ist an der Grenze die N dotierte Schicht positiv geladen und die P Schicht negativ geladen.
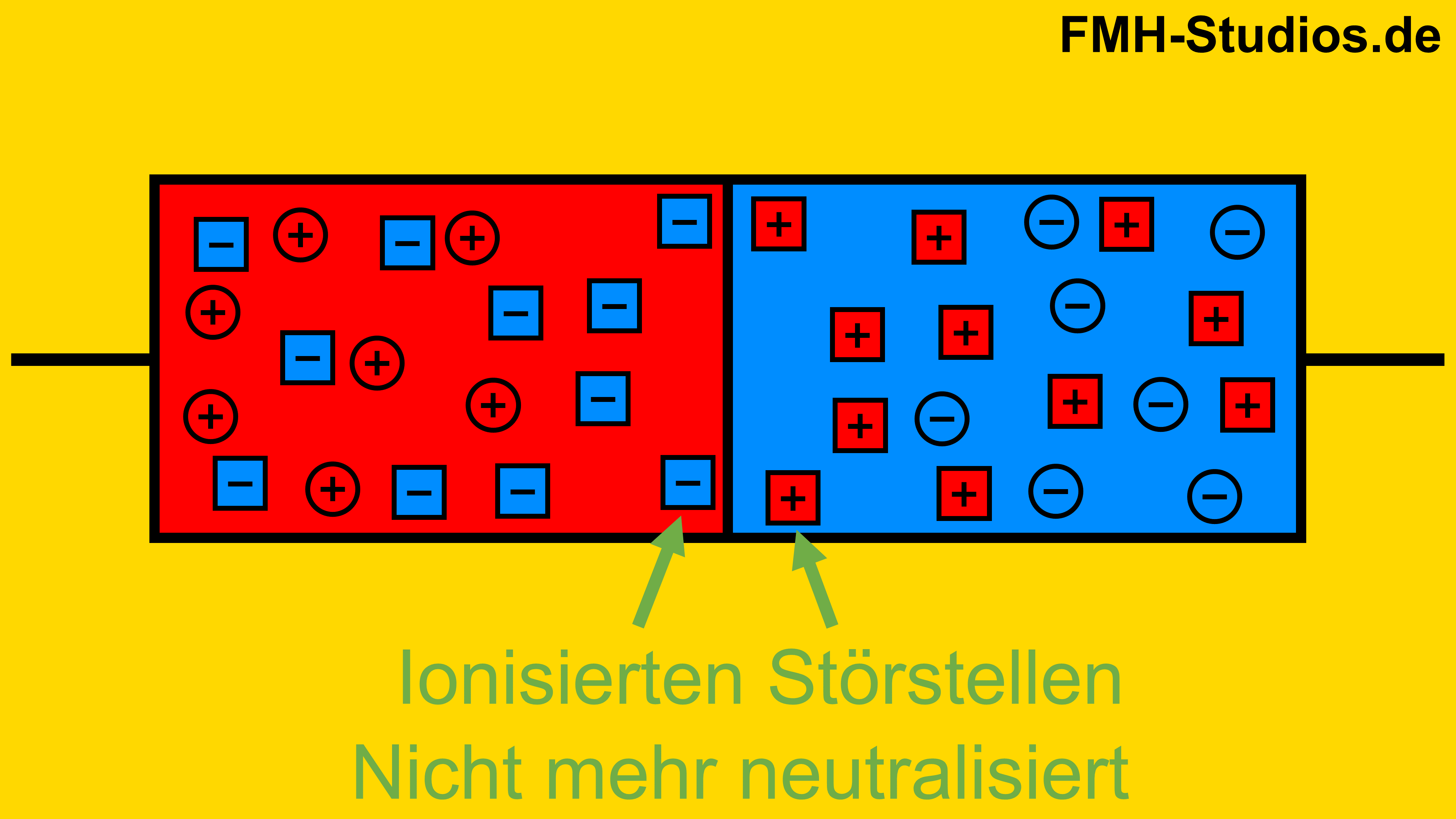
Aus den Grundlagen ist bereits bekannt, dass eine negative und eine positive Ladung ein elektrisches Feld zur Folge hat. So besteht auch hier ein elektrisches Feld zwischen N und P Dotierter Zone (An der Grenze).
Diese Spannung wird als Diffusionsspannung bezeichnet.
Je mehr Ladungsträger rekombinieren, desto weiter steigt die Diffusionsspannung an.
Die Diffusionsspannung ist dem Diffusionsstrom entgegengesetzt – wirkt also der Diffusion der Ladungsträger entgegen.
Durch die Diffusionsspannung entsteht der Driftstrom. Dieser fließt in entgegengesetzte Richtung wie der Diffusionsstrom.
Hierdurch breitet sich die Raumladungszone auch nicht immer weiter aus.
Die Diffusionsspannung in der Anwendung
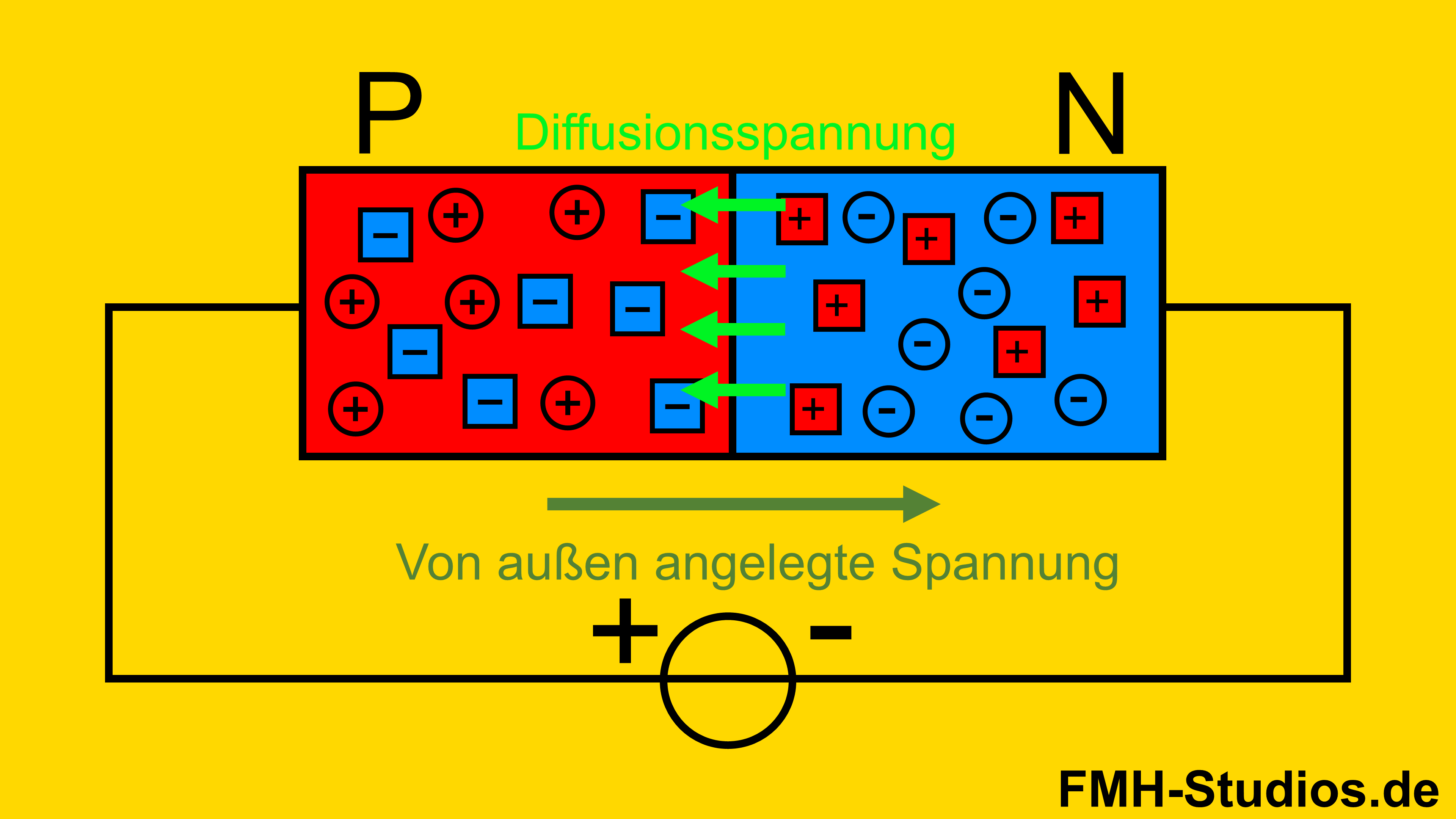
Beim Verwenden der Diode / des PN-Übergangs in der Praxis spielt die Diffusionsspannung eine wichtige Rolle. Wie bereits bekannt, funktioniert die Diode in der Elektronik ähnlich wie ein Ventil.
⇨ Grundlagen zur Diode
Damit aber in Vorwärtsrichtung ein hoher Strom fließt, muss erstmal eine bestimmte mindest Spannung vorliegen. Dies ist auch an der Kennlinie zu erkennen. Bei einer Silizium-Diode fängt erst ab ~0,7V Vorwärtsspannung an Strom zu fließen.
⇨ Diodenkennlinie
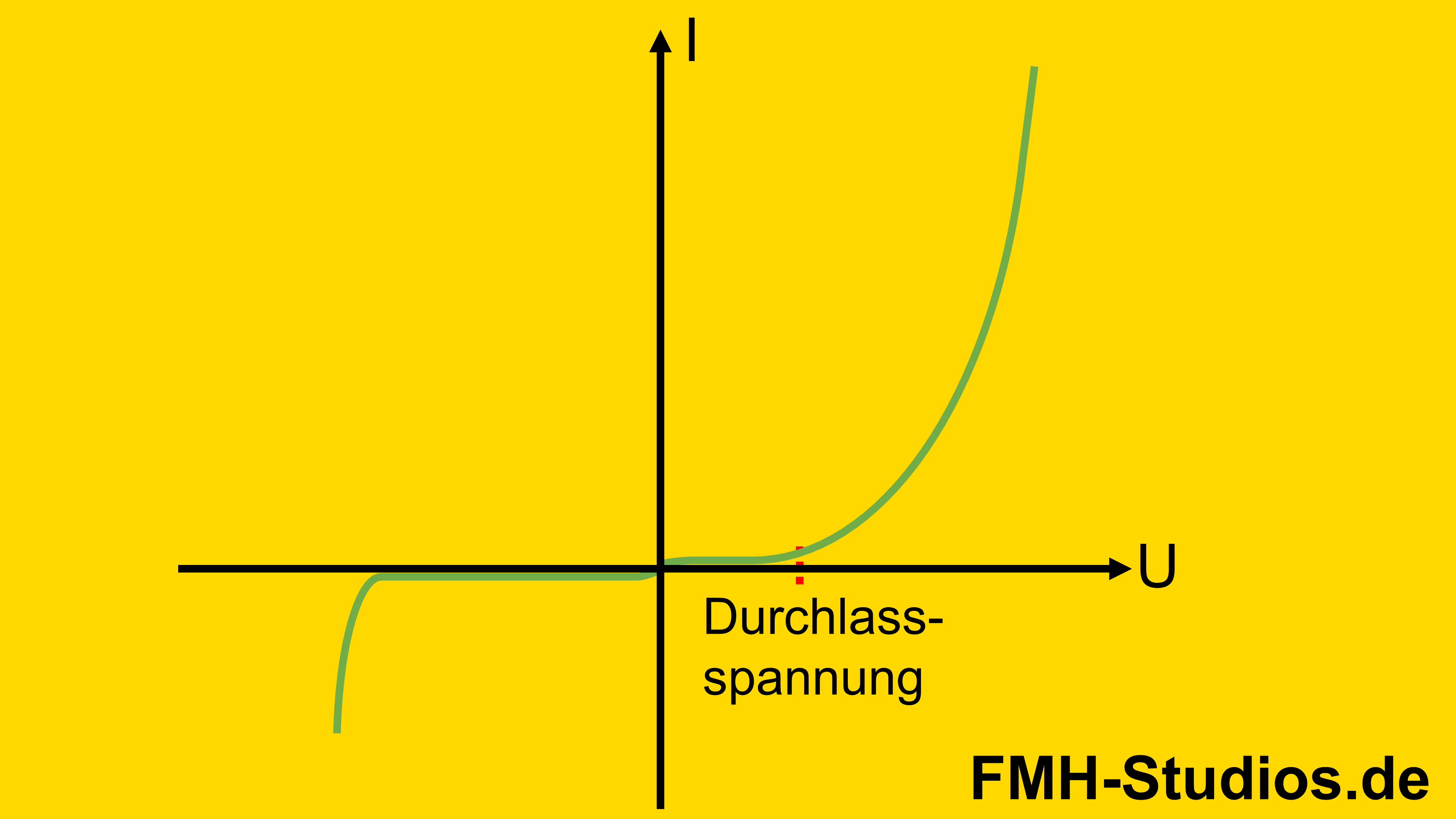
Es muss erst die Diffusionsspannung überwunden werden, damit ein hoher Strom durch die Diode fließen kann.
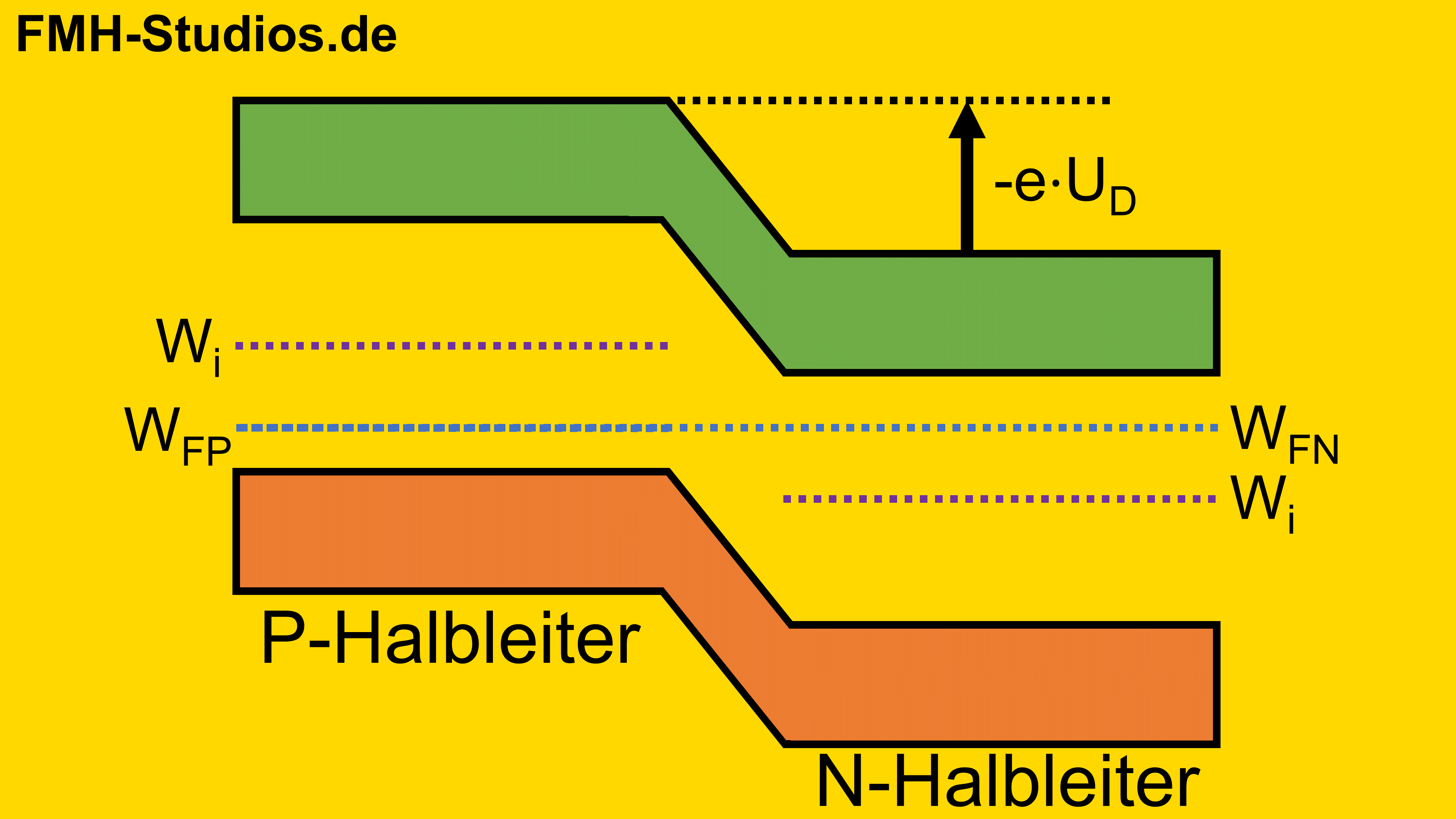
Diffusionsspannung im Bändermodell
Die Diffusionsspannung lässt sich auch im Bändermodell darstellen. Hierfür schauen wir uns das Bändermodell des PN-Übergang / der Diode an. Wie wir bereits wissen, gleichen sich beim Zusammenfügen von N und P dotierten Halbleiter das Fermi-Niveaus an.
Das bedeutet, die getrennt betrachteten Bändermodelle von N- und P-Halbleiter verschieben sich. Dabei ergibt sich die Spannung aus der Differenz der beiden Leitungsband Oberkanten.
Berechnung der Diffusionsspannung
Mit der unten stehenden Gleichung lässt sich die Diffusionsspannung berechnen.
Hierbei ist sie natürlich abhängig vom intrinsischen Halbleiter und der Dotierung. Dies ist auch in der Gleichung zu sehen.
Die Dotierdichte fließt mit der Dichte der Akzeptoren (nA) und der Dichte der Donatoren (nD) ein.
Während die Eigenleitungsdichte (ni) abhängig ist vom intrinsischen Halbleitermaterial. (Germanium: ni= 2,3 ⋅ 10^13 cm^-3)
Die Spannung UT ist die Temperaturspannung. Entsprechend ist die Diffusionsspannung auch abhängig von der Temperatur.
Wie zu sehen, hängt die Diffusionsspannung nur wenig von der Dotierung ab. Der Zusammenhang ist logarithmisch. Das bedeutet sogar bei einer Verzehnfachung der Dotierung ergibt sich eine Änderung von nur 0,026 V ln(100) = 0,12 V.
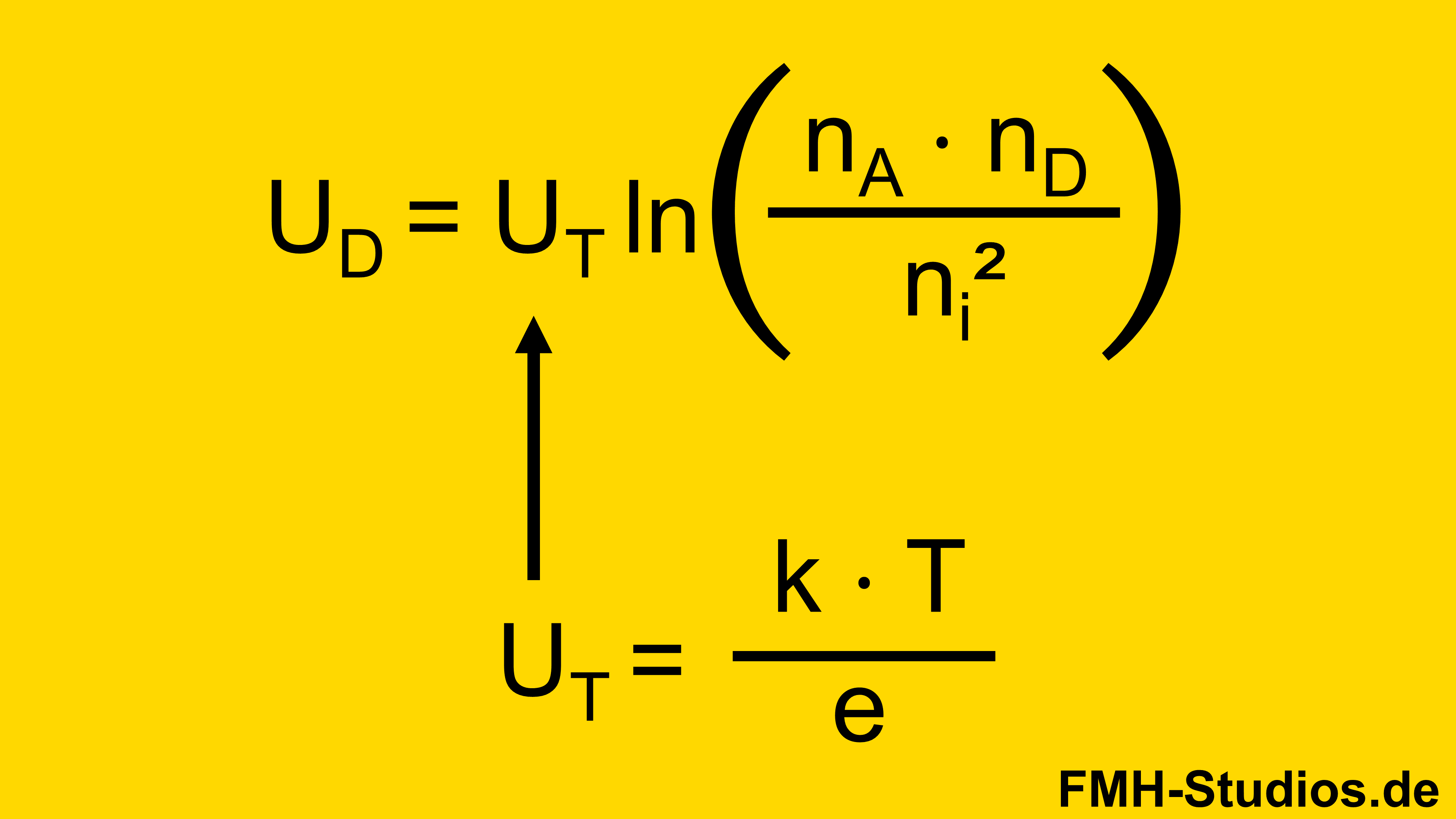
Typische Werte der Diffusionsspannung
Der Wert der Diffusionsspannung hängt vom Halbleitermaterial ab. Wird Silizium als Halbleiterelement verwendet, liegt diese bei ~0,7V. Bei Germanium bei ~0,3V.
Messung der Diffusionsspannung
Die Diffusionsspannung kann von außen nicht gemessen werden.
Denn wenn die äußeren Kontakte (oder die Kontakte der Spannungsmessung) aus Metall bestehen, bildet sich eine Diffusionsspannung gleicher Größe an der Grenzschicht zwischen Metall und Halbleiter. Allerdings ist diese Diffusionsspannung mit umgekehrter Polarität – also in entgegengesetzter Richtung, wie die Diffusionsspannung am PN-Übergang entgegengerichtet.
Die Summe der Spannungen ist Null und kann daher nicht gemessen werden.
⇨ Metall Halbleiter Übergang